Chapter 4: Listening Tests (Pt 2)

Chapter 4: Listening Tests, Part II

Section 1. In this section, listeners sat in the center position with their heads voluntarily motionless and listened to noise bursts panned by each algorithm around the circle in 36º increments. These were stationary pans of the noise bursts.

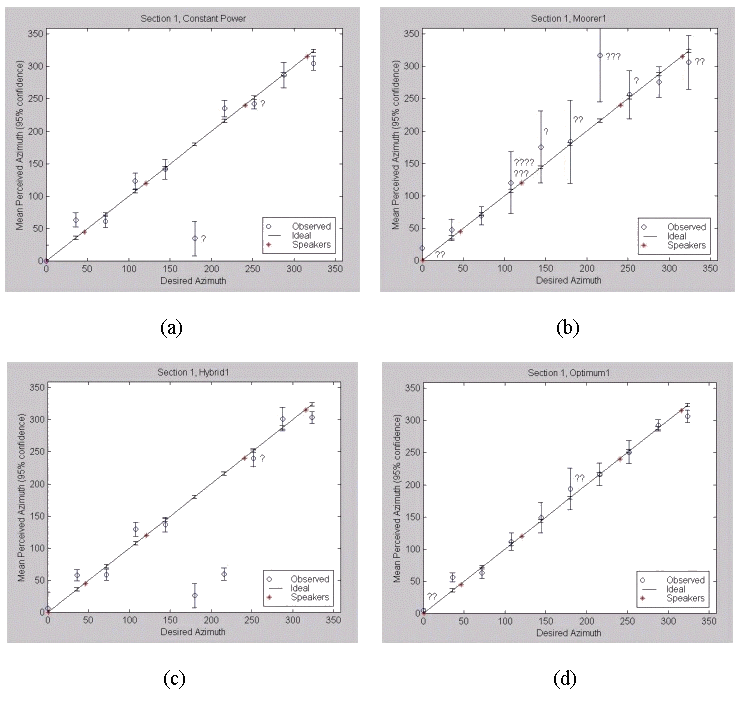
We can make some statistical inferences with 95% confidence where the observed and ideal confidence intervals do not overlap in Figure 4.10.

Fig. 4.10. Section 1 Results: (a) Constant Power, (b) Moorer, (c) Hybrid, (d) Gerzon Optimal.

In the constant power plot, Figure 4.10 (a), the confidence interval is greatest at 180º. Recall that confidence intervals are directly proportional to the standard deviations. The large standard deviation and error from the ideal mean at 180º are a sign of front-back confusion. The noise bursts around the L and SR speakers seem to be pulled towards the direction of the speakers. The two question marks indicate that only twice was a listener not able to localize the noise bursts at all.

In the Moorer plot, Figure 4.10 (b), the standard deviations tend to be much larger than those in the constant power algorithm, especially between 108º and 252º. A listener was not able to localize the noise bursts at all a total of 18 (out of 110) times. Note that at 108º, seven out of eleven listeners could not localize the sound at all.

The reader should recall that each hybrid panning plot should look like the constant power and optimal panning plots in the regions from 45º to 315º and 315º to 45º, respectively. In Figure 4.10 (c), the confidence intervals are comparable to those of constant power panning. The large errors from the ideal mean at 180º and 216º are a sign of front-back confusion. The noise bursts around the L, SL and R speakers seem to be pulled towards the direction of the speakers. Only once could a listener not localize the noise bursts.

In the optimal plot, Figure 4.10 (d), the confidence intervals tend to be a little larger than in constant power panning, especially between the SL and SR speakers (144º, 180º, and 216º). Interestingly, there is an absence of a large error from the ideal mean at 180º. While a large confidence interval exists at 180º (~ 70º), there seems to be less of a front-back confusion problem than in constant power panning. The noise bursts around the L and (somewhat the) R speakers seem to be pulled towards the direction of the speakers. A listener could not localize the noise bursts at all four separate times.

Section 2. In this section, listeners sat in the center position with their heads free to move. They listened to ten noise bursts panned by each algorithm around the circle in 36º increments. These were stationary pans of the noise bursts.

In the constant power plot, Figure 4.11 (a), the confidence intervals tend to be a little smaller and the mean errors a little smaller than those for constant power panning in section 1. (By "mean error", we mean the difference between the closest edges of the confidence intervals of the observed and ideal azimuths.) However, large mean errors and confidence intervals at both 0º and 180º indicate that front-back confusion is evident now at both angles. This is a significant change from all plots in section 1. The noise bursts around the L and SR speakers seem to be pulled towards the direction of the speakers. Only twice was a listener not able to localize the noise bursts.

The confidence intervals and thus standard deviations for Moorer panning are again very large compared with constant power panning. Front-back confusion is evident at 0º and possibly 216º. This is very comparable with the Moorer plot from section 1 (Figure 4.10 (b)). A listener was not able to localize the noise bursts at all 27 (out of 110) separate times.

The hybrid panning algorithm, Figure 4.11 (c), is very comparable to that in section 1 (Figure 4.10 (c)). Very surprisingly, it does not show front-back confusion at 0º (as does optimal panning in this section). It also shows a "wider" front-back confusion arc (including 180º and 216º) than constant power panning from this section. Again, we expect no difference between the hybrid algorithm and the optimum and constant power algorithms for their respective piecewise regions in the hybrid algorithm. Only twice was a listener not able to localize the noise bursts.

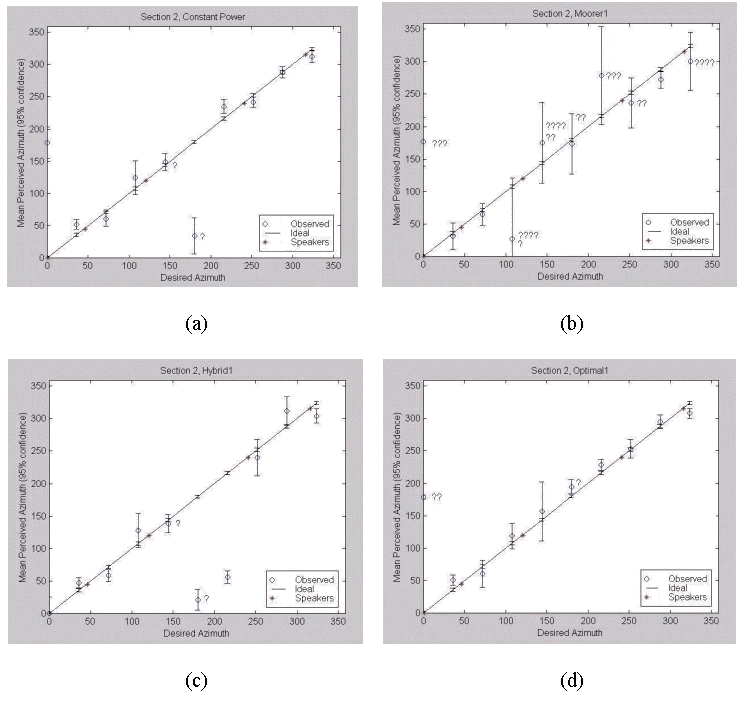
Fig. 4.11. Section 2 Results: (a) Constant Power, (b) Moorer, (c) Hybrid, (d) Gerzon Optimal.

The optimal panning algorithm, Figure 4.11 (d), shows the same front-back confusion at 0º as the constant power plot from this section. The optimal panning algorithm plots in section 1 and 2 both show no tendency for front-back reversal at 180º. The optimal algorithm from this section shows slightly larger confidence intervals compared with the optimal and constant power algorithm plots from section 1 (Figure 4.10 (a) and (d), respectively). The noise bursts around the L and R speakers seem to be pulled towards the direction of the speakers. Only three times was a listener not able to localize the noise bursts.

Section 3. In this section, listeners sat in the center position with their heads voluntarily motionless. They listened to fifteen noise bursts whose motion was panned around the circle in 90º arcs. Due to an error in transferring digital audio files from Matlab to Deck 2.6, one of the original 16 moving pan recordings was not included in the test as planned. This means that data from the constant power moving pan from 270º to 359º (region 4) is not available for analysis. A crude guess at the scores for this data point in the speed, distance, and width scores would be an average of the optimal and constant power scores for this region.

The scores in section 3 range from 1 to 10 and indicate the consistency of speed, distance, or width as the noise burst is panned 90º around the listener. The reader should recall that these form a ratio scale, so a score of 10 is twice as consistent as a score of 5. Recall also that scores for each listener were recentered to 5 in sections 3 and 6.

Unfortunately, the confidence intervals, and thus standard deviations, are very large throughout both sections. Almost all inferences that can be made cannot be said with 95% confidence. The choice was made to use the 90% confidence criterion, thus making the confidence intervals smaller and less likely to overlap.

From the speed scores, Figure 4.12 (a), we see that all panning algorithms performed similarly (i.e., much confidence interval overlap). In region 2, the Moorer algorithm performed worse than both the constant power and optimal algorithms. The hybrid algorithm showed about twice the standard deviation than the others in region 2, and about half the standard deviation in region 4.

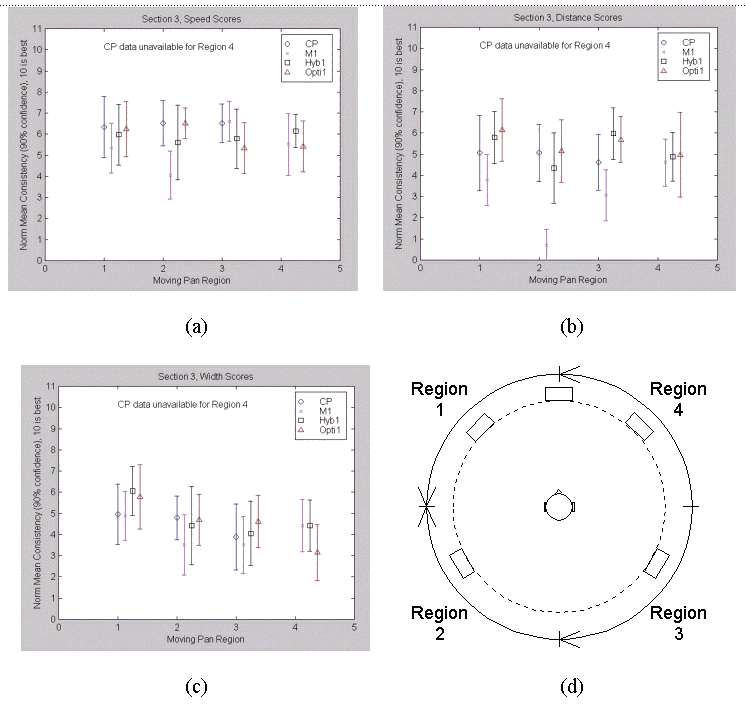
Fig. 4.12. Section 3 Results: Scores for (a) speed, (b) distance, (c) width, (d) moving pan regions.

Standard deviations tended to be larger for the distance scores than the speed scores. Figure 4.12 (b) shows the distance scores. The Moorer algorithm performed significantly worse than the others in region 2, and worse than the hybrid and optimal algorithms in region 3.

Figure 4.12 (c) shows the mean width scores. These tended to be fairly similar between the algorithms but generally lower than both the speed and distance scores.

Section 4. In this section, listeners sat off-center by two feet with their heads voluntarily motionless. They listened to noise bursts panned by each algorithm around the circle in 36º increments. These were stationary pans of the noise bursts.

The constant power plot, Figure 4.13 (a), should be compared with that from the center listening position with a motionless head (Figure 4.10 (a)). The plot from this section tends to have (1) slightly larger confidence intervals and (2) observed means that are slightly closer to the ideal mean. (As expected, the means azimuths here generally follow the curve for ideal off-center listening.) The front-back confusion at 180º (but not 0º) is evident. A listener was not able to localize the noise bursts at all 6 separate times.

When we compare the Moorer algorithm plot in Figure 4.13 (b) to that in section 1 (Figure 4.10 (b)), we see that the confidence intervals here get bigger for the middle angles (108º to 180º especially). There is now front-back confusion at 0º, and what must be a more confusing reversal at 140º and 180º. Compared with the constant power plot from Figure 4.13 (a), this plot tends to have much larger confidence intervals. A listener was not able to localize the noise bursts 30 (out of 110 possible) times. (At three of the angles, more than half of the listeners were not able to localize the noise bursts.)

The hybrid algorithm in Figure 4.13 (c) performed fairly well, with the exception of a front-back reversal only at 180º. A listener was not able to localize the noise bursts 4 times.

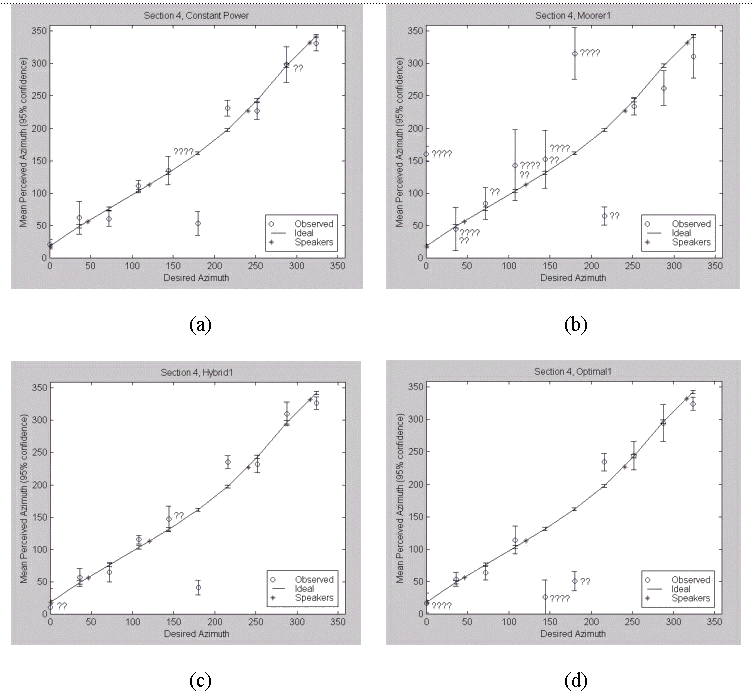
Fig. 4.13. Section 4 Results: (a) Constant Power, (b) Moorer, (c) Hybrid, (d) Gerzon Optimal.

The strength of the optimum panning algorithm in the center listening position (Figure 4.10 (d)), namely a lack of front-back confusion at 180º, is now absent. This is a significant and unfortunate change of behavior. A front-back reversal now exists at 180º, and it covers a wider arc than the constant power plot from this section (Figure 4.13 (a)). A listener was not able to localize the noise bursts at all 10 separate times (6 in the front-back reversal region).

Section 5. In this section, listeners sat off-center by two feet with their heads free to move. They listened to ten noise bursts panned by each algorithm around the circle in 36º increments. These were stationary pans of the noise bursts.

The constant power plot, Figure 4.14 (a), is very similar to that in section 4 (off-center, head motionless, Figure 4.13 (a)). They are very similar except that the confidence intervals in this section are generally smaller. In this case, the ability to turn one’s head generally improved the listeners’ localization ability. Only once was a listener not able to localize the noise bursts.

The Moorer algorithm, Figure 4.14 (b), can be similarly compared to that in section 4 (Figure 4.13 (b)). The confidence intervals tend to get smaller with the ability to turn one’s head. There is still a front-back reversal at 0º and a milder one at 180º. As with all the Moorer plots, the confidence intervals tend to get fairly large between 108º and 180º. A listener was not able to localize the noise bursts at all 13 separate times.

The hybrid algorithm, Figure 4.14 (c), is very similar to that in section 4 (Figure 4.13 (c)), except that the front-back reversal area is wider. Interestingly, this doesn’t show up in the constant power algorithm in this section (Figure 4.14 (a)), which is exactly the same algorithm in this region. Only twice was a listener not able to localize the noise bursts.

The optimal algorithm, Figure 4.14 (d), is very similar to that in section 4 (Figure 4.13 (d)). It has the same wide front-back reversal region between 144º and 180º, and its confidence intervals have gotten just a little smaller in general. Even though the listeners were two feet closer to the R and SR speakers, the mean localization for phantom images between these speakers (at 252 and 288º) were dead on. This was better than the case when listeners were not able to move their heads (Figure 4.13 (d)). Only three times was a listener not able to localize the noise bursts at all.

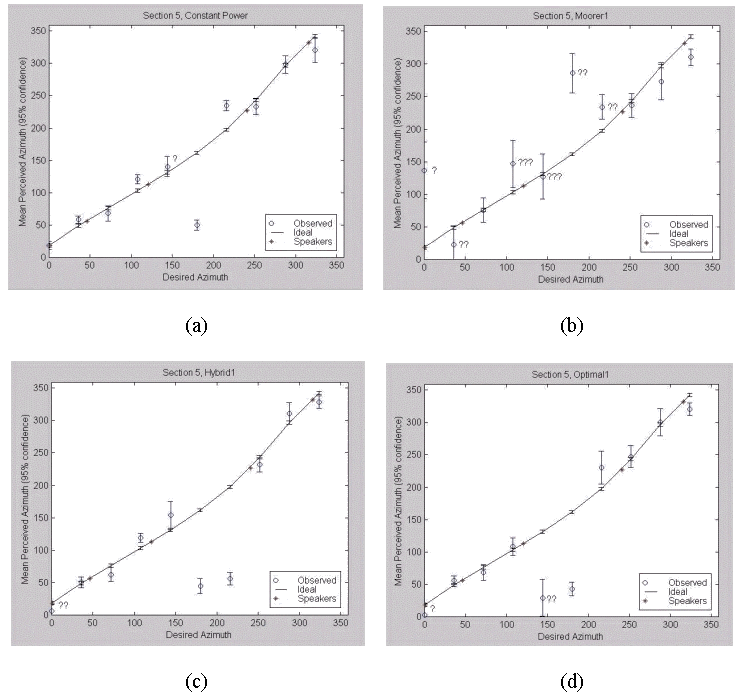
Fig. 4.14. Section 5 Results: (a) Constant Power, (b) Moorer, (c) Hybrid, (d) Gerzon Optimal.

Section 6. In this section, listeners sat in off-center by 2 ft with their heads voluntarily motionless. They listened to fifteen noise bursts whose motion was panned around the circle in 90º arcs.

Fig. 4.15. Section 6 Results: Scores for (a) speed, (b) distance, (c) width, (d) moving pan regions.

Speed scores for off-center seating in Figure 4.15 (a) are difficult to compare to those from the center position (Figure 4.12 (a)). Standard deviations for all algorithms tended to be a little larger. In the off-center position, the Moorer algorithm performed better in region 2, and worse in regions 3 and 4 (esp. compared with the optimal algorithm in region 3). The optimal algorithm tended to behave better in the rear soundstage (regions 2 and 3) compared to its score in section 3 and to all other algorithms in this section.

Next we compare the distance scores from Figure 4.15 (b) to those in the center listening position (section 3, Figure 4.12 (b)). The scores for all algorithms were lower in regions 2 and 4. The Moorer algorithm performed worse than all algorithms in region 1 and generally worse in region 2 as well. All scores for region 3 were more similar than they were in section 3.

The width scores from Figure 4.15 (c) were generally higher than those in section 3 (Figure 4.12 (c)). The different algorithms performed similarly in all regions for this section, with the exception that the Moorer algorithm performed worse than all the others in region 2. Scores for the optimal algorithm were just barely better than the others in regions 2, 3, and 4.

Interpretations

The constant power algorithm shows standard deviations similar in magnitude to those seen with optimal panning. Localization is good but not perfect. The hybrid algorithm is no better than either the constant power or optimal algorithm. In fact, it does not incorporate the main strength of the optimal algorithm -- few if any front-back reversals for the center listening position. The optimal algorithm is superior to the other algorithms in the center listening position because of low mean errors and the lack of a front-back confusion problem. Unfortunately, the front-back reversals show up in the off-center position and cover a wider range of rear angles than off-center constant power panning. The Moorer algorithm showed poor performance in all tests. Standard deviations and errors of the mean azimuths tended to be very high, indicating listener confusion while localizing sounds panned with this method. Recall that Willcocks et al. [36] predicted better localization for pair-wise panning algorithms (such as constant power) in the off-center position compared with non-pair-wise algorithms (such as the optimal and Moorer algorithms). (See their quote at the end of Chapter 3.)

Mean scores for the moving pan tests generally were not separated enough to draw any significant conclusions. The only algorithm that showed significantly different performance was the Moorer algorithm, which scored significantly lower several times.

Within the scope and limitations of this test, the Moorer algorithm is not a suitable method of surround sound panning in its current implementation. The hybrid algorithm is not superior to either the constant power or optimum algorithm. Within the scope and limitations of this test, constant power panning and optimal 5-channel panning perform the best of all four algorithms. The final choice between the two must be made based on the application and other quality criteria described in Chapter 3. Constant power and optimum panning both will be implemented in software since there is no clear winner between them based on the listening test results.

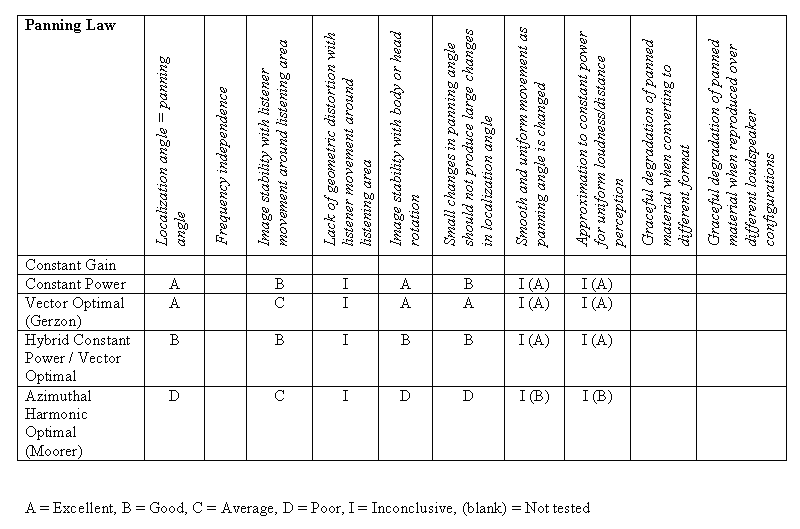
Table 4.10 summarizes the results of the listening tests by giving each algorithm a very coarse letter grade for each of the tested pan pot criteria.

Table 4.10. Experimental comparison of panning algorithms using Gerzon's criteria

(Previous Chapter) <- Main Page -> (Next Chapter)